Class field theory

In mathematics, class field theory is a major branch of algebraic number theory that studies abelian extensions of number fields.

Most of the central results in this area were proved in the period between 1900 and 1950. The theory takes its name from the fact that the field extensions it studies, such as the Hilbert class field, are associated to classes of ideals, so are called class fields. The ideal class group (which is a basic object of study inside a single field of numbers K, such as a quadratic field), is also seen as a Galois group of a field extension L/K: L is a field containing K and all the roots of a polynomial with coefficients in K.

These days the term is generally used synonymously with the study of all the abelian extensions of algebraic number fields, or more generally of local fields and global fields; an abelian extension being a Galois extension with Galois group that is an abelian group (a finite abelian extension of Q is often simply called an abelian number field). In general terms, the objective is either to construct extensions of this type for a general number field K, or, to predict their arithmetical properties in terms of the arithmetical properties of K itself.

Contents

Formulation in contemporary language

In modern language there is a maximal abelian extension A of K, which will be of infinite degree over K; and associated to A a Galois group G which will be a pro-finite group, so a compact topological group, and also abelian. The central aim of the theory is to describe G in terms of K.

The fundamental result of class field theory states that the group G is naturally isomorphic to the profinite completion of the idele class group CK of K with respect to the natural topology on CK (i.e. not the profinite completion of CK as an abstract group). Equivalently, for any finite Galois extension L of K, there is an isomorphism

Gal(L / K)ab → CK / NL/K CL

of the maximal abelian quotient of the Galois group of the extension with the quotient of the idele class group of K by the image of the norm of the idele class group of L.[1]

For example when K is the field of rational numbers the abelianized absolute Galois group G of K is (naturally isomorphic to) an infinite product of the group of units of the p-adic integers taken over all prime numbers p, and the corresponding maximal abelian extension of the rationals is the field generated by all roots of unity. This is known as the Kronecker–Weber theorem, originally conjectured by Leopold Kronecker.

In case K = 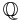\Q, the isomorphism of class field theory (i.e. the reciprocity map, or Artin reciprocity) also admits an explicit description due to the Kronecker–Weber theorem, which states that the maximal abelian extension of 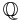\Q is given by adjoining all roots of unity to 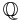\Q. Let us denote with

\mu_\infty \subset \C^\times

the group of all roots of unity, i.e. the torsion subgroup. The Artin reciprocity map is given by

\hat{{\Z}}^\times \to G_\Q^{\rm ab} = {\rm Gal}(\Q(\mu_\infty)/\Q), \quad x \mapsto (\zeta \mapsto \zeta^x),

when it is arithmetically normalized, or given by

\hat{{\Z}}^\times \to G_\Q^{\rm ab} = {\rm Gal}(\Q(\mu_\infty)/\Q), \quad x \mapsto (\zeta \mapsto \zeta^{-x}),

if it is geometrically normalized.

For a description of the general case see class formation.

Prime ideals

More than just the abstract description of G, it is essential for the purposes of number theory to understand how prime ideals decompose in the abelian extensions. The description is in terms of Frobenius elements, and generalises in a far-reaching way the quadratic reciprocity law that gives full information on the decomposition of prime numbers in quadratic fields. The class field theory project included the 'higher reciprocity laws' (cubic reciprocity and so on), but is not limited to that one, classical, line of generalisation.

History

The origins of class field theory lie in the quadratic reciprocity law proved by Gauss. The generalisation took place as a long-term historical project, involving quadratic forms and their 'genus theory', work of Ernst Kummer and Leopold Kronecker/Kurt Hensel on ideals and completions, the theory of cyclotomic and Kummer extensions, conjectures of David Hilbert, the reciprocity laws, and proofs by numerous mathematicians (Teiji Takagi, Helmut Hasse, Emil Artin, Phillip Furtwängler and others). The crucial Takagi existence theorem was known by 1920 and all the main results by about 1930. One of the last classical conjectures to be proved was the principalisation property. The first proofs of class field theory used substantial analytic methods. An important step was the introduction of ideles by Claude Chevalley whose use essentially clarified and simplified structures which describe abelian extensions of global fields.

In the 1930s and subsequently the use of infinite extensions and the theory of Wolfgang Krull of their Galois groups was found increasingly useful. It combines with Pontryagin duality to give a clearer if more abstract formulation of the central result, the Artin reciprocity law. It is also basic to Iwasawa theory.

After the results were reformulated in terms of group cohomology which became a standard way to learn class field theory for several generations of number theorists. One drawback of the cohomological method is its relative inexplicitness. As the result of contributions of John Tate, Michiel Hazewinkel, Jurgen Neukirch and also due to the work on explicit reciprocity formulas by many mathematicians, a very explicit and cohomology free presentation of class field theory was established in the nineties, see e.g. the book of Neukirch.

One of attempts to develop a more general class field theory which describes non-abealian extensions of global fields is the Langlands program. Its development in the sixties and seventies provided a fresh impetus, and it is often viewed as 'non-abelian class field theory', though that description does not include any kind of existence theorem and does not provide as much arithmetical information as the abelian class field theory.

See also

References

  1. ^ (Neukirch 1999, Theorems VI.5.5, VI.6.1)